Part 1: Imbalanced species data, background points, and weighting methods

Author details: Xiang Zhao

Editor details: Dr Sebastian Lopez Marcano

Contact details: support@ecocommons.org.au

Copyright statement: This script is the product of the EcoCommons platform. Please refer to the EcoCommons website for more details: https://www.ecocommons.org.au/

Date: February 2025

Script and data info

This notebook, developed by the EcoCommons team, showcases how to deal with imbalanced species datasets (presence and absence data) with weighting methods.

Abstract (Part 1 and Part 2)

When building species distribution models, it is common to encounter imbalanced datasets. This may involve a large number of presence records and relatively few absence records, or, in the case of rare species, a substantial number of absence records but only a limited number of presence records.

When working with imbalanced datasets, models and predictions can be prone to several issues, including bias towards the majority class, misleading performance metrics, and reduced sensitivity to the minority class. This occurs because the model learns predominantly from the more frequent class, leading to poor generalisation for rare events (Menardi & Torelli, 2014). Therefore, it is essential to address dataset imbalance to ensure fair and reliable predictions.

This notebook explores strategies to address the challenges posed by imbalanced species data in ecological modeling, particularly in Species Distribution Models (SDMs). It focuses on the use of background points and weighting methods to improve model performance when presence and absence data are disproportionate. This notebook examines the effectiveness of different pseudo-absence generation techniques, including random and buffered-random background point sampling, and applies weighting schemes to mitigate class imbalance. Using the Gang-gang Cockatoo (Callocephalon fimbriatum) as a case study, the analysis demonstrates the impact of these methods on model evaluation metrics such as AUROC, AUPR, F1-score, and TSS. This guide aims to equip ecologists and data scientists with practical approaches for handling imbalanced datasets, ensuring more accurate and reliable SDMs within the EcoCommons platform.

Objectives (Part 1)

  1. Understand what imbalanced datasets are and their influence on model performance
  2. Understand how weighting methods can help address the issue of imbalanced datasets.

Workflow Overview:

  • Set the working directory and load the necessary R packages. Create directories to store raw data files.

  • Data Download: Download prepared imbalanced dataset(s) from the EcoCommons Google Drive.

  • Data preparation and split.

  • Model evaluation and comparison.

In the near future, this material may form part of comprehensive support materials available to EcoCommons users. If you have any corrections or suggestions to improve the effeciengy, please contact the EcoCommons team.

Set-up: R Environment and Packages

Some housekeeping before we start. This process might take some time as many packages needed to be installed.

S.1 Set the working directory and create a folder for data.

Save the Quarto Markdown file (.QMD) to a folder of your choice, and then set the path to your folder as your working directory.

# Set the workspace to the current working directory

workspace <- getwd()  # Get the current working directory and store it in 'workspace'

# Increase the plot size by adjusting the options for plot dimensions in the notebook output
options(repr.plot.width = 16, repr.plot.height = 8)  # Sets width to 16 and height to 8 for larger plots

Ideally, you would use the renv package to create an isolated environment for installing all the required R packages used in this notebook. However, since installing renv and its dependencies can be time-consuming, we recommend trying this after the workshop.

# # Ensure "renv" package is installed
# if (!requireNamespace("renv", quietly = TRUE)) {
#   install.packages("renv")
# }
# 
# # Check if renv has been initialised in the project
# if (!file.exists("renv/activate.R")) {
#   message("renv has not been initiated in this project. Initializing now...")
#   renv::init()  # Initialise renv if not already set up
# } else {
#   source("renv/activate.R")  # Activate the renv environment
#   message("renv is activated.")
# }
# 
# # Check for the existence of renv.lock and restore the environment
# if (file.exists("renv.lock")) {
#   message("Restoring renv environment from renv.lock...")
#   renv::restore()
# } else {
#   message("No renv.lock file found in the current directory. Skipping restore.")
# }

S.2 Install and load essential libraries.

Install and load R packages.

# Set CRAN mirror
options(repos = c(CRAN = "https://cran.rstudio.com/"))

# List of packages to check, install if needed, and load
packages <- c("dplyr", "reshape2", "terra", "sf", "googledrive", "ggplot2", "corrplot", 
              "pROC", "dismo", "spatstat.geom", "patchwork", "biomod2", "PRROC",
              "leaflet", "car", "gridExtra", "htmltools", "RColorBrewer", "kableExtra", "tibble")

# Function to display a cat message
cat_message <- function(pkg, message_type) {
  if (message_type == "installed") {
    cat(paste0(pkg, " has been installed successfully!\n"))
  } else if (message_type == "loading") {
    cat(paste0(pkg, " is already installed and has been loaded!\n"))
  }
}

# Install missing packages and load them
for (pkg in packages) {
  if (!requireNamespace(pkg, quietly = TRUE)) {
    install.packages(pkg)
    cat_message(pkg, "installed")
  } else {
    cat_message(pkg, "loading")
  }
  library(pkg, character.only = TRUE)
}
dplyr is already installed and has been loaded!
reshape2 is already installed and has been loaded!
terra is already installed and has been loaded!
sf is already installed and has been loaded!
googledrive is already installed and has been loaded!
ggplot2 is already installed and has been loaded!
corrplot is already installed and has been loaded!
pROC is already installed and has been loaded!
dismo is already installed and has been loaded!
spatstat.geom is already installed and has been loaded!
patchwork is already installed and has been loaded!
biomod2 is already installed and has been loaded!
PRROC is already installed and has been loaded!
leaflet is already installed and has been loaded!
car is already installed and has been loaded!
gridExtra is already installed and has been loaded!
htmltools is already installed and has been loaded!
RColorBrewer is already installed and has been loaded!
kableExtra is already installed and has been loaded!
tibble is already installed and has been loaded!
# If you are using renv, you can snapshot the renv after loading all the packages.

#renv::snapshot()

S.3 Download case study datasets

We have prepared the following data and uploaded them to our Google Drive for your use:

  • Species occurrence data: Shapefile format (.shp)

  • Environmental variables: Stacked Raster format (.tif)

  • Study area boundary: Shapefile format (.shp)

# De-authenticate Google Drive to access public files
drive_deauth()

# Define Google Drive file ID and the path for downloading
zip_file_id <- "1GXOA330Ow2F7NqxdhuBfbz0a-CMT8DTb" 

datafolder_path <- file.path(workspace)

# Create a local path for the zipped file
zip_file_path <- file.path(datafolder_path, "imbalanced_data.zip")

# Function to download a file with progress messages
download_zip_file <- function(file_id, file_path) {
  cat("Downloading zipped file...\n")
  drive_download(as_id(file_id), path = file_path, overwrite = TRUE)
  cat("Downloaded zipped file to:", file_path, "\n")
}

# Create local directory if it doesn't exist
if (!dir.exists(datafolder_path)) {
  dir.create(datafolder_path, recursive = TRUE)
}

# Download the zipped file
cat("Starting to download the zipped file...\n")
Starting to download the zipped file...
download_zip_file(zip_file_id, zip_file_path)
Downloading zipped file...
Downloaded zipped file to: /Users/xiangzhaoqcif/Documents/QCIF_MacBook_Pro/github/notebook-blog/notebooks/data_prep/imbalanced_data.zip 
# Unzip the downloaded file
cat("Unzipping the file...\n")
Unzipping the file...
unzip(zip_file_path, exdir = datafolder_path)
cat("Unzipped files to folder:", datafolder_path, "\n")
Unzipped files to folder: /Users/xiangzhaoqcif/Documents/QCIF_MacBook_Pro/github/notebook-blog/notebooks/data_prep

1. Introduction

1.1 Imbalanced binary species dataset

Imbalanced datasets are common. As shown in the figure below, a dataset is considered imbalanced when the classifications are not equally represented (Chawla et al., 2002).

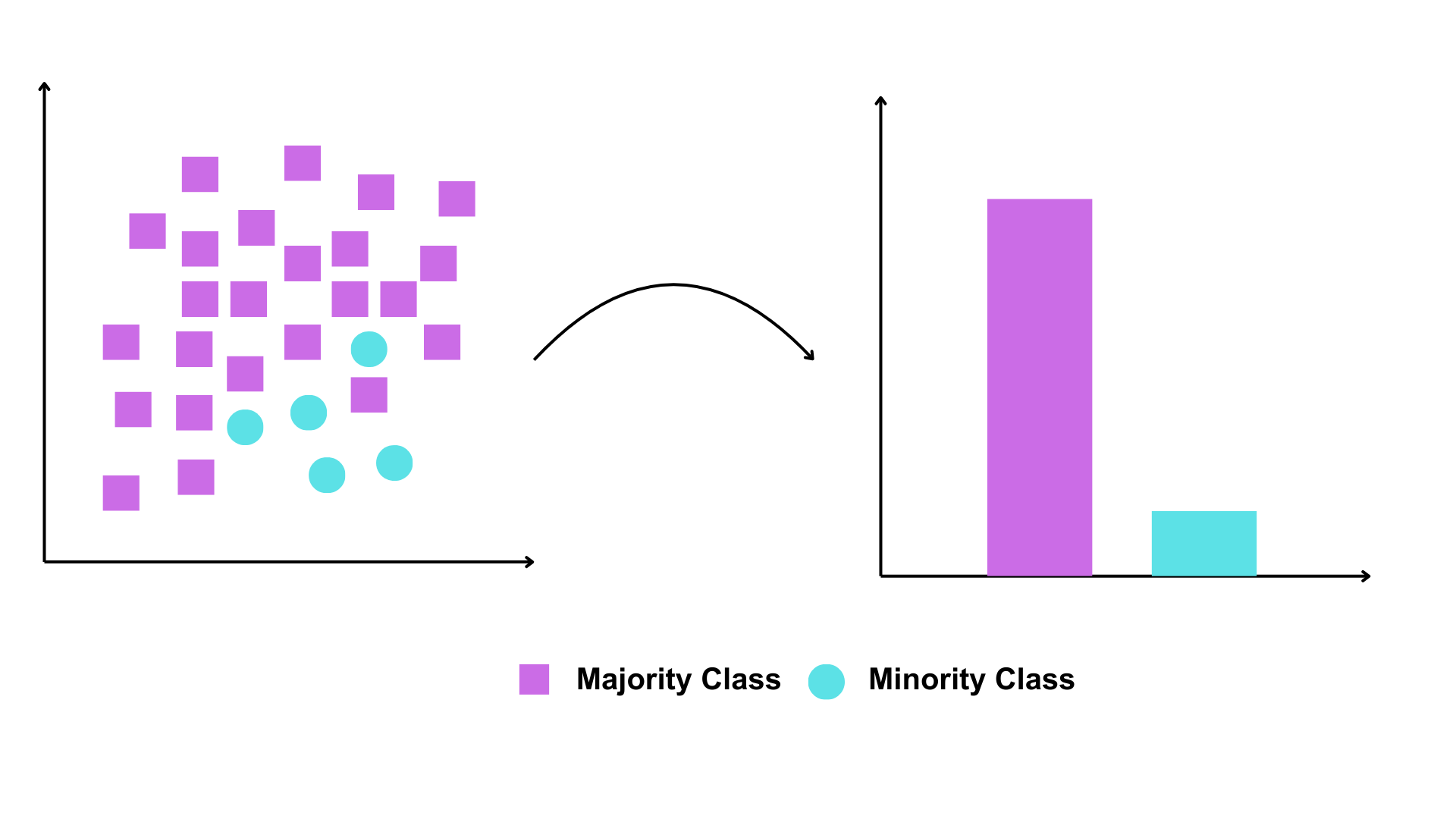
In binary species records, where data consists of presence and absence observations, a common challenge is dataset imbalance—specifically, an overabundance of presence records. This phenomenon is prevalent in many biodiversity data portals, where most species have only presence records and lack corresponding absence data.

When using an imbalanced dataset, modelling and prediction can lead to biased outcomes. For example, if presence records dominate the training set, the model may be more likely to predict presence to minimise overall errors. This can result in high sensitivity (true positive rate, correctly identifying most presences) but low specificity (true negative rate, failing to identify absences) (Johnson et al., 2012).

Therefore, addressing dataset imbalance before fitting SDMs is a crucial step to ensure reliable predictions.

1.2 Weighting methods

Many studies have shown that weighting methods can improve SDM performance (Benkendorf et al., 2023; Chen et al., 2004; Zhang et al., 2020). By applying class weights to SDM algorithms, the cost of misclassifying the minority class can be increased relative to the cost of misclassifying the majority class (Benkendorf et al., 2023).

For example, if a dataset contains 900 presences and 100 absences, the class ratio is 9:1. To compensate for this imbalance, class weights can be assigned inversely proportional to class frequencies. In this case, a weight of 1 would be assigned to the majority class (presences) and a weight of 9 to the minority class (absences). This means the model incurs a 9× cost for misclassifying an absence compared to a presence. Such reweighting has been shown to improve the tradeoff between model sensitivity and specificity. Specifically, while increases in sensitivity often come at the expense of specificity and overall accuracy, applying class weights can help achieve a better balance.

In this notebook, we use a simple weighting method employed by Elith et al. (Elith* et al., 2006) and Valavi et al. (Valavi et al., 2022). The weights are assigned by giving a weight of 1 to each presence location and adjusting the background weights so that the total weight of presence and background samples is equal.

# Load necessary library
library(dplyr)

# 1️⃣ Create a toy dataset
set.seed(123)  # For reproducibility

# Example data frame with presence (1) and background/absence (0)
train_data <- data.frame(
  id = 1:10,
  occrrnS = c(rep(1, 7), rep(0, 3))  # 7 presence points, 3 background points
)

# 2️⃣ Calculate weights
# Count the number of presence and background points
prNum <- sum(train_data$occrrnS == 1)
bgNum <- sum(train_data$occrrnS == 0)

# Apply weights: presence = 1, background = prNum / bgNum
wt <- ifelse(train_data$occrrnS == 1, 1, prNum / bgNum)

# Add weights to the data frame
train_data <- train_data %>%
  mutate(weight = wt)

# 3️⃣ Display the final dataset with weights
print(train_data)
   id occrrnS   weight
1   1       1 1.000000
2   2       1 1.000000
3   3       1 1.000000
4   4       1 1.000000
5   5       1 1.000000
6   6       1 1.000000
7   7       1 1.000000
8   8       0 2.333333
9   9       0 2.333333
10 10       0 2.333333

The sum of the weights for 1 (Present) is 7 × 1 = 7, which is equal to the sum of the weights for 0 (Absent), 2.33 × 3 = 7. This weighting method will be used to address the imbalanced dataset issue in this notebook.

1.4 Evaluation metric

Several studies suggest how to evaluate the model performance of imbalanced dataset (Barbet-Massin et al., 2012; Gaul et al., 2022; Johnson et al., 2012; Zhang et al., 2020). We select these to use in this notebook:

We also provide some information on model evaluation on our platform’s educational material page.
Metric What it Tells You Optimised When
AUROC (Area Under ROC Curve) Ability of the model to distinguish between classes When overall discriminative power is important
CORR (Correlation between the observation in the occurrence dataset and the prediction) Degree of correlation between predicted and observed values When assessing the strength and direction of relationships
Precision Proportion of positive predictions that are correct False positives need to be minimised
Recall Ability to capture actual positives Missing positives has severe consequences
Specificity Ability to correctly identify negatives False positives need to be minimised
F1-Score Balance between Precision and Recall Both false positives and false negatives are costly
AUPR (Area Under Precision-Recall Curve) Performance on imbalanced datasets focusing on positive class When positive class is rare and critical
TSS (True Skill Statistic) Skill of the model beyond random chance When evaluating presence/absence models in ecological studies

2 Overview and Conceptualisation

2.1 Model and notebook objective

⚠️This notebook focuses not on creating a perfect Species Distribution Model (SDM) for the Gang-gang Cockatoo, but on comparing different methods for addressing class imbalance in binary species datasets and evaluating their effectiveness in improving SDM performance.⚠️

2.2 Taxon, location, data, scale, and model algorithm

Taxon: Gang-gang Cockatoo (Callocephalon fimbriatum)

Gang-gang

Photographer: Kym Nicolson, ALA

The Gang-gang Cockatoo (Callocephalon fimbriatum) is endemic to southeastern Australia, with its distribution primarily spanning higher elevations and southern latitudes, including regions in New South Wales, Victoria, and the Australian Capital Territory. It inhabits temperate eucalypt forests and woodlands, favoring wet sclerophyll forests with dense acacia and banksia understories during the summer months, while moving to drier, open woodlands at lower altitudes in winter. The species is well-adapted to cooler climates and often forages in parks and suburban gardens.

Gang-gang Cockatoos face significant threats, including habitat loss due to land clearing, wildfire damage, and competition for nesting hollows with other species. Climate change, particularly increased fire frequency and altered rainfall patterns, has introduced additional risks to their survival. The species has experienced a drastic population decline, further exacerbated by the 2019–2020 bushfires, which burned approximately 28–36% of its habitat, leading to a projected long-term decline in population size.

Location: Australian Capital Territory (ACT, study area)

Spatial and temporal scales: small (spatial) and static (temporal)

Model algorithm: Generalised linear model (GLM)

2.3 Imbalanced biodiversity data

Understanding your species is essential. This includes knowing their common names (which may include multiple names) and scientific name to ensure you collect the most comprehensive records available in open-access biodiversity data portals, such as the Atlas of Living Australia (ALA) or the Global Biodiversity Information Facility (GBIF).

For this exercise, we have prepared a species occurrence data file in CSV format, which was downloaded from ALA. To make it accessible, we have stored this file in the EcoCommons Google Drive for you to download and use conveniently.

# Read the shapefile for Gang-gang Cockatoo occurrence point dataset
gang_gang_act <- st_read("imbalanced_data/gang_gang_ACT.shp")
Reading layer `gang_gang_ACT' from data source 
  `/Users/xiangzhaoqcif/Documents/QCIF_MacBook_Pro/github/notebook-blog/notebooks/data_prep/imbalanced_data/gang_gang_ACT.shp' 
  using driver `ESRI Shapefile'
Simple feature collection with 918 features and 1 field
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: 148.77 ymin: -35.9 xmax: 149.39 ymax: -35.13
Geodetic CRS:  GDA94
# Read the shapefile for ACT dataset
ACT <- st_read("imbalanced_data/ACT_4283.shp")
Reading layer `ACT_4283' from data source 
  `/Users/xiangzhaoqcif/Documents/QCIF_MacBook_Pro/github/notebook-blog/notebooks/data_prep/imbalanced_data/ACT_4283.shp' 
  using driver `ESRI Shapefile'
Simple feature collection with 1 feature and 0 fields
Geometry type: POLYGON
Dimension:     XY
Bounding box:  xmin: 148.7628 ymin: -35.92053 xmax: 149.3993 ymax: -35.12442
Geodetic CRS:  GDA94
# Create leaflet map
leaflet() %>%
  addProviderTiles(providers$Esri.WorldImagery) %>%
  
  # Add the ACT layer with a distinct color
  addPolygons(
    data = ACT,
    color = "lightblue",         # Border color of ACT polygon
    weight = 1,                  # Border width
    fillColor = "lightblue",      # Fill color of ACT
    fillOpacity = 0.3,           # Transparency for fill
    group = "ACT"
  ) %>%
  
  # Add Gang-gang Cockatoo presence/absence points from the same shapefile
  addCircleMarkers(
    data = gang_gang_act,
    color = ~ifelse(occrrnS == "PRESENT", "#11aa96", "#f6aa70"),  # Dynamically set color based on occrrnS
    radius = 1,
    weight = 0.5,
    opacity = 1,
    fillOpacity = 1,
    group = "Gang-gang Cockatoo Records"
  ) %>%
  
  setView(lng = 149, lat = -35.5, zoom = 8) %>% # Set the view to desired location
  
  # Add layer controls for toggling
  addLayersControl(
    overlayGroups = c("ACT", "Gang-gang Cockatoo Records"),
    options = layersControlOptions(collapsed = FALSE)
  ) %>%
  
  # Add a legend for the layers
  addControl(
    html = "
    <div style='background-color: white; padding: 10px; border-radius: 5px;'>
      <strong>Legend</strong><br>
      <i style='background: lightblue; width: 18px; height: 18px; display: inline-block; margin-right: 8px; opacity: 0.7;'></i>
      ACT Boundary<br>
      <i style='background: #11aa96; width: 10px; height: 10px; border-radius: 50%; display: inline-block; margin-right: 8px;'></i>
      Gang-gang Cockatoo Presence<br>
      <i style='background: #f6aa70; width: 10px; height: 10px; border-radius: 50%; display: inline-block; margin-right: 8px;'></i>
      Gang-gang Cockatoo Absence
    </div>
    ",
    position = "bottomright"
  )

Now, let’s calculate the number of presences and absences in the dataset to assess the extent of imbalance.

# Calculate counts of presence (PRESENT) and absence (ABSENT)
occ_counts <- table(gang_gang_act$occrrnS)

# Convert to data frame for plotting
occ_df <- as.data.frame(occ_counts)
colnames(occ_df) <- c("Occurrence", "Count")

# Create bar plot with custom colors
ggplot(occ_df, aes(x = Occurrence, y = Count, fill = Occurrence)) +
  geom_bar(stat = "identity") +
  geom_text(
    aes(label = Count),
    vjust = -0.3,  
    size = 3
  ) +
  labs(
    title = "Presence vs Absence Count",
    x = "Occurrence",
    y = "Count"
  ) +
  scale_fill_manual(values = c("PRESENT" = "#11aa96", "ABSENT" = "#f6aa70")) +
  theme_minimal()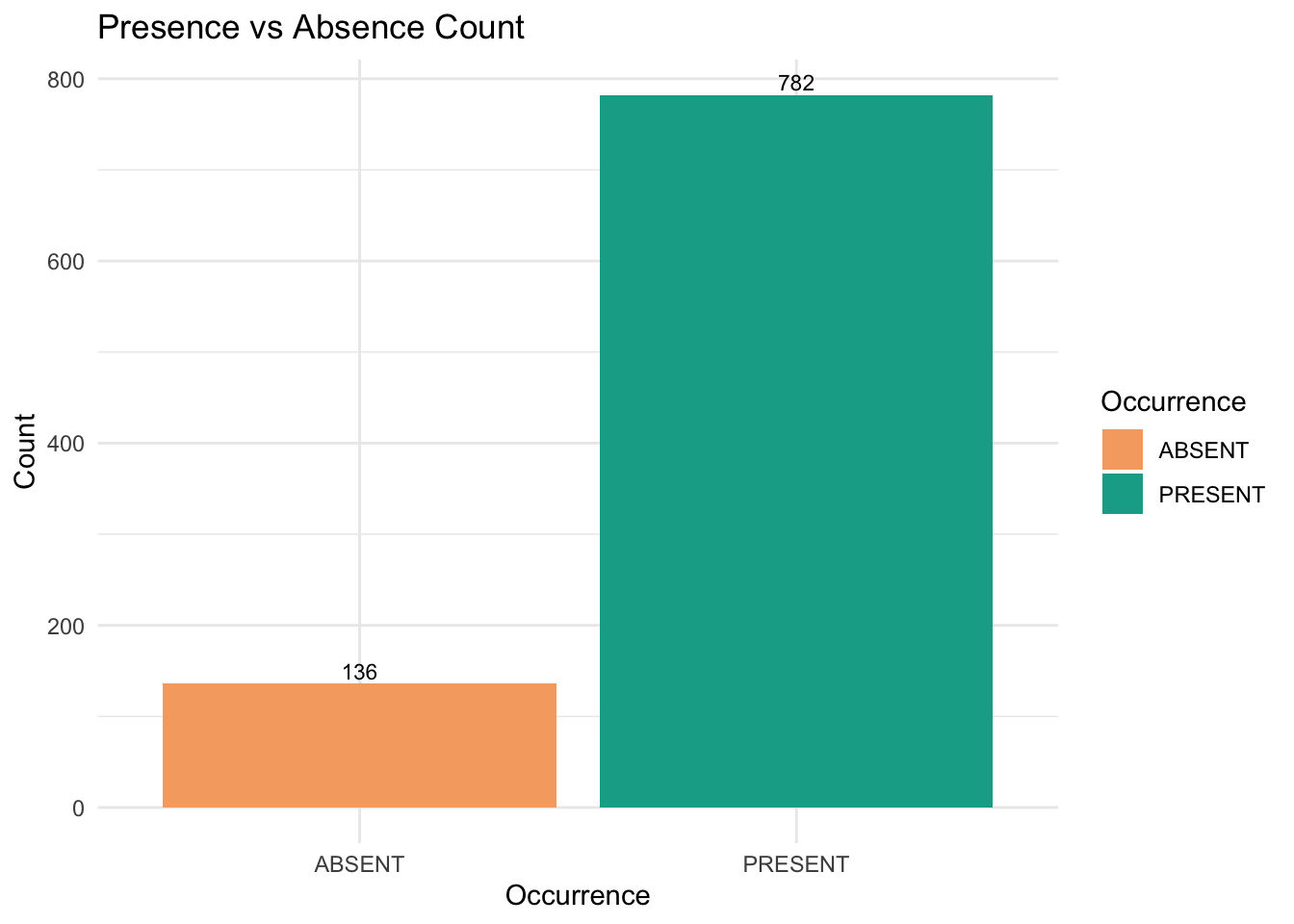

We can see the amount of Gang-gang Cockatoo absent records are way less than its present records.

2.4 Environmental variables

We conducted several tests and selected seven environmental variables for this case study. For more information on preparing environmental datasets and selecting environmental variables, please refer to our notebooks: Raster-preparation and GLM (section 2.3-3.1).

Variable code Description
AusClim_bioclim_03_9s_1976-2005 Isothermality (BIO3) — Mean Diurnal Range / Annual Temp Range × 100
AusClim_bioclim_06_9s_1976-2005 Min Temperature of Coldest Month (BIO6)
AusClim_bioclim_09_9s_1976-2005 Mean Temperature of Driest Quarter (BIO9)
AusClim_bioclim_15_9s_1976-2005 Precipitation Seasonality (Coefficient of Variation) (BIO15)
AusClim_bioclim_24_9s_1976-2005 Annual Mean Moisture Index (custom or derived bioclim variable)
AusClim_bioclim_27_9s_1976-2005 Mean Moisture Index of Driest Quarter (custom/derived)
AusClim_bioclim_29_9s_1976-2005 Mean Radiation of Warmest Quarter (custom/derived) 
# Load the stacked raster layers
env_var_stack <- rast("imbalanced_data/ACT_raster.tif")

# Select the desired layers by their names
selected_layers <- c("AusClim_bioclim_03_9s_1976-2005",
                     "AusClim_bioclim_06_9s_1976-2005",
                     "AusClim_bioclim_09_9s_1976-2005",
                     "AusClim_bioclim_15_9s_1976-2005",
                     "AusClim_bioclim_24_9s_1976-2005",
                     "AusClim_bioclim_27_9s_1976-2005",
                     "AusClim_bioclim_29_9s_1976-2005")

# Subset the raster stack
selected_rasters <- env_var_stack[[selected_layers]]

# Plot all selected layers
plot(selected_rasters, main = "Selected Environmental Variables", cex.main = 0.8)

3. When we have true-absence data

3.1 Including true absence in the training dataset

Including true-absence data in training dataset is always recommended when such data is available (Václavı́k & Meentemeyer, 2009). In this study, we aim to explore the question: ‘how much true-absence data is enough?’ ‘Is more always better?’

To answer this question, we allocate 90%, 70%, 50% of the true absence data, along with an equal amount of present data to the test dataset, using the rest data as training dataset.

Here, we can make a function to split the data as we want.

split_occurrence_data_by_absence_test <- function(data, p_abs_test = 0.9, seed = 123) {
  # Set seed for reproducibility
  set.seed(seed)
  
  # Identify indices for ABSENT and PRESENT rows
  abs_idx <- which(data$occrrnS == "ABSENT")
  pres_idx <- which(data$occrrnS == "PRESENT")
  
  # Total number of ABSENT records
  n_abs <- length(abs_idx)
  
  # Number of ABSENT records to include in test set
  n_test_abs <- round(p_abs_test * n_abs)
  
  # Randomly sample n_test_abs indices from the ABSENT indices for the test set
  test_abs_idx <- sample(abs_idx, n_test_abs)
  
  # For the test set, randomly sample an equal number of PRESENT records
  test_pres_idx <- sample(pres_idx, n_test_abs)
  
  # Create test data: sampled ABSENT + sampled PRESENT
  test_data <- data[c(test_abs_idx, test_pres_idx), ]
  
  # Create training data: the remaining rows (i.e., those not selected for test)
  train_data <- data[-c(test_abs_idx, test_pres_idx), ]
  
  return(list(test_data = test_data, train_data = train_data))
}

Now, we can use the above function to split the data in three difference ways:

  • 90% of true absence data, along with an equal amount of present data to the test dataset, using the rest data as training dataset.

  • 70% of true absence data, along with an equal amount of present data to the test dataset, using the rest data as training dataset.

  • 50% of the true absence data, along with an equal amount of present data to the test dataset, using the rest data as training dataset.

# For a 90% test split (of the ABSENT records)
split_90_absence <- split_occurrence_data_by_absence_test(gang_gang_act, p_abs_test = 0.9, seed = 123)

# For a 70% test split
split_70_absence <- split_occurrence_data_by_absence_test(gang_gang_act, p_abs_test = 0.7, seed = 123)

# For a 50% test split
split_50_absence <- split_occurrence_data_by_absence_test(gang_gang_act, p_abs_test = 0.5, seed = 123)

# Generate counts from the split data
train_90_absence <- table(split_90_absence$train_data$occrrnS)
test_90_absence <- table(split_90_absence$test_data$occrrnS)

train_70_absence <- table(split_70_absence$train_data$occrrnS)
test_70_absence <- table(split_70_absence$test_data$occrrnS)

train_50_absence <- table(split_50_absence$train_data$occrrnS)
test_50_absence <- table(split_50_absence$test_data$occrrnS)

# Create a data frame with the extracted counts
split_data <- data.frame(
  Split = c("90% Absence Train", "90% Absence Test", "70% Absence Train", "70% Absence Test", "50% Absence Train", "50% Absence Test"),
  ABSENT = c(train_90_absence["ABSENT"], test_90_absence["ABSENT"],
             train_70_absence["ABSENT"], test_70_absence["ABSENT"],
             train_50_absence["ABSENT"], test_50_absence["ABSENT"]),
  PRESENT = c(train_90_absence["PRESENT"], test_90_absence["PRESENT"],
              train_70_absence["PRESENT"], test_70_absence["PRESENT"],
              train_50_absence["PRESENT"], test_50_absence["PRESENT"])
)

# Display the table
print(split_data)
              Split ABSENT PRESENT
1 90% Absence Train     14     660
2  90% Absence Test    122     122
3 70% Absence Train     41     687
4  70% Absence Test     95      95
5 50% Absence Train     68     714
6  50% Absence Test     68      68

We can visualise above table in a bar chart.

# Reshape data for ggplot using melt
split_data_melted <- melt(split_data, id.vars = "Split", variable.name = "Status", value.name = "Count")

# Create the bar plot with labels
ggplot(split_data_melted, aes(x = Split, y = Count, fill = Status)) +
  geom_bar(stat = "identity", position = position_dodge(width = 0.9)) +  # Adjust bar positions
  geom_text(aes(label = Count), 
            position = position_dodge(width = 0.9), 
            vjust = -0.5, size = 3) +  # Add text labels
  labs(title = "ABSENT and PRESENT Counts Across Data Splits", x = "Data Split", y = "Count") +
  theme_minimal() +
  scale_fill_manual(values = c("ABSENT" = "#f6aa70", "PRESENT" = "#11aa96")) +
  theme(axis.text.x = element_text(angle = 45, hjust = 1)) +
  theme(legend.title = element_blank())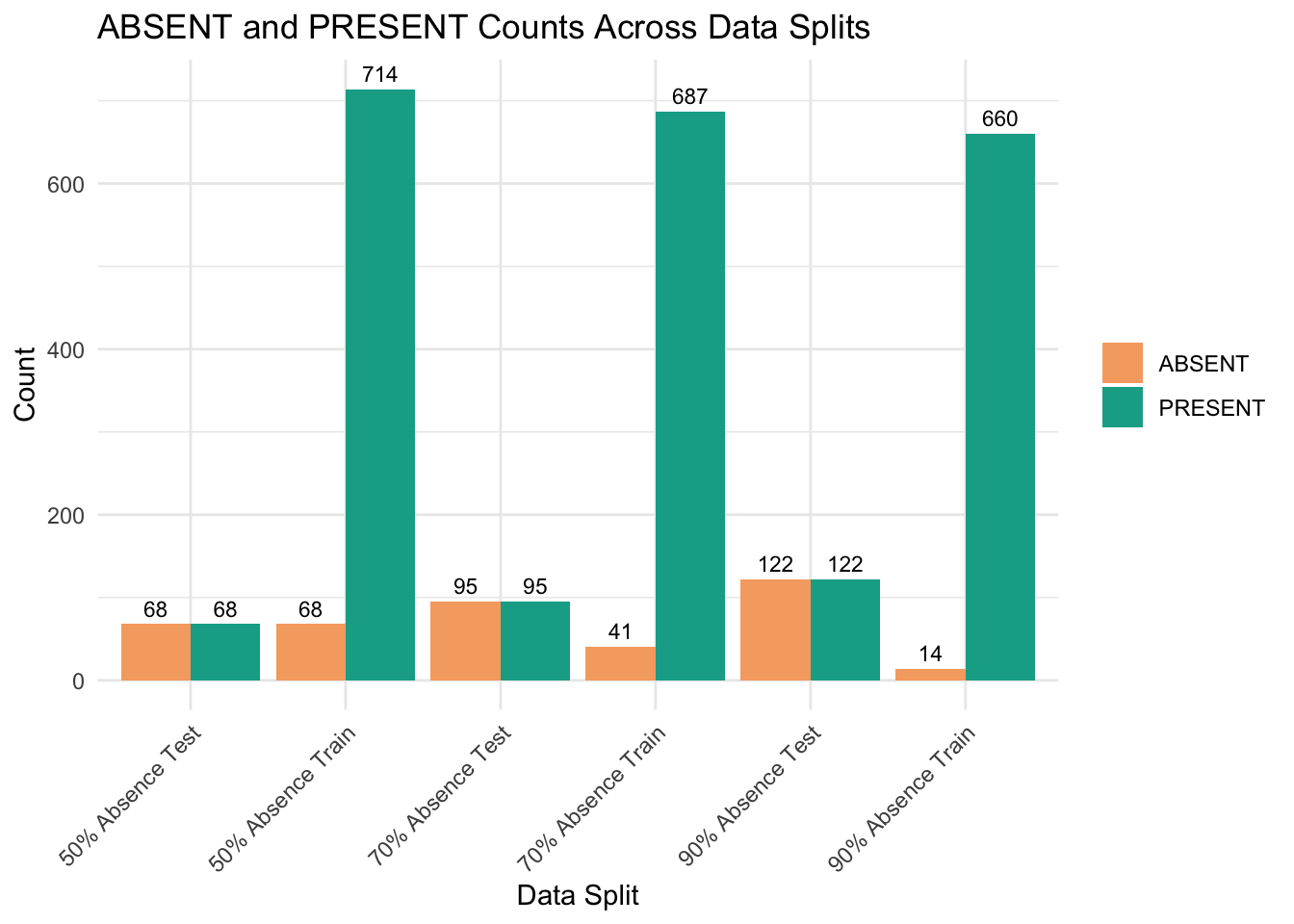

Now, we combine the training and test data with environmental dataset.

get_occurrence_data <- function(occurrence_sf, env_var_stack, drop_na = TRUE, dropCols = NULL) {
  # Convert the occurrence sf object to a terra SpatVector
  occ_vect <- vect(occurrence_sf)
  
  # Extract raster values at the occurrence points
  extracted_values <- terra::extract(env_var_stack, occ_vect)
  
  # Combine occurrence data (as a data frame) with the extracted raster values
  occ_data <- cbind(as.data.frame(occurrence_sf), extracted_values)
  
  # Optionally remove rows with any NA values
  if (drop_na) {
    occ_data <- na.omit(occ_data)
  }
  
  # Optionally drop specified columns
  if (!is.null(dropCols)) {
    occ_data <- occ_data[, -dropCols]
  }
  
  return(occ_data)
}
combine_with_env_data <- function(split_list, env_var_stack, dropCols = c(2,3)) {
  # Process the training data
  train_data_env <- get_occurrence_data(split_list$train_data, env_var_stack, dropCols = dropCols)
  # Process the test data
  test_data_env  <- get_occurrence_data(split_list$test_data, env_var_stack, dropCols = dropCols)
  
  return(list(train_data_env = train_data_env, test_data_env = test_data_env))
}
# Then, combine each split with the environmental variables:
env_combined_90 <- combine_with_env_data(split_90_absence, env_var_stack, dropCols = c(2,3))

env_combined_70 <- combine_with_env_data(split_70_absence, env_var_stack, dropCols = c(2,3))

env_combined_50 <- combine_with_env_data(split_50_absence, env_var_stack, dropCols = c(2,3))

# Create a list of three training data data frames
train_list <- list(
  "split_90_train" = env_combined_90$train_data_env,
  "split_70_train" = env_combined_70$train_data_env,
  "split_50_train" = env_combined_50$train_data_env
)

# Create a list of three training data data frames
test_list <- list(
  "split_90_test" = env_combined_90$test_data_env,
  "split_70_test" = env_combined_70$test_data_env,
  "split_50_test" = env_combined_50$test_data_env
)

Now, we have three sets of training and test data ready for modelling.

  • split_90_train & split_90_test

  • split_70_train & split_70_test

  • split_50_train & split_50_test

3.2 Un-weighted models

In this section, we will ignore the issue of dataset imbalance and run a GLM SDM model. We will generate all the evaluation metrics mentioned in section 1.4 Evaluation metric.

This is a function running GLM and producing evaluation metrics.

fit_model_and_get_perf_no_wt <- function(train_data_env, test_data_env, tss_step = 0.01) {
  
  # Load required libraries
  library(pROC)     # For AUROC
  library(PRROC)    # For AUPR
  
  # 1) Copy data locally
  train_data <- train_data_env
  test_data  <- test_data_env
  
  # Convert occrrnS to 0/1 numeric
  train_data$occrrnS <- ifelse(train_data$occrrnS == "PRESENT", 1, 0)
  test_data$occrrnS  <- ifelse(test_data$occrrnS == "PRESENT", 1, 0)
  
  # Define model formula
  my_formula <- occrrnS ~ `AusClim_bioclim_03_9s_1976-2005` + 
    `AusClim_bioclim_06_9s_1976-2005` + 
    `AusClim_bioclim_09_9s_1976-2005` + 
    `AusClim_bioclim_15_9s_1976-2005` + 
    `AusClim_bioclim_24_9s_1976-2005` + 
    `AusClim_bioclim_27_9s_1976-2005` + 
    `AusClim_bioclim_29_9s_1976-2005`
  
  # 2) Fit the unweighted GLM model
  model <- glm(my_formula, data = train_data, family = binomial(link = "logit"))
  
  # Predict probabilities on the test data
  predicted_probs <- predict(model, newdata = test_data, type = "response")
  
  # -----------------------------
  # PART A: Standard metrics at threshold = 0.5
  # -----------------------------
  pred_class <- ifelse(predicted_probs >= 0.5, 1, 0)
  
  # Force table to have both '0' and '1' as levels
  pred_class_factor <- factor(pred_class, levels = c(0,1))
  actual_factor     <- factor(test_data$occrrnS, levels = c(0,1))
  
  conf_mat <- table(Predicted = pred_class_factor, Actual = actual_factor)
  
  # Safely extract entries
  TP <- conf_mat["1","1"]
  FP <- conf_mat["1","0"]
  FN <- conf_mat["0","1"]
  TN <- conf_mat["0","0"]
  
  accuracy    <- (TP + TN) / sum(conf_mat)
  sensitivity <- TP / (TP + FN)  # Recall
  specificity <- TN / (TN + FP)
  precision   <- TP / (TP + FP)
  f1          <- 2 * precision * sensitivity / (precision + sensitivity)
  
  # -----------------------------
  # PART B: Additional Metrics
  # -----------------------------
  
  # AUROC
  roc_curve <- pROC::roc(response = test_data$occrrnS, predictor = predicted_probs)
  auc_value <- pROC::auc(roc_curve)
  
  # AUPR (Area Under Precision-Recall Curve)
  pr <- pr.curve(scores.class0 = predicted_probs[test_data$occrrnS == 1],
                 scores.class1 = predicted_probs[test_data$occrrnS == 0],
                 curve = TRUE)
  aupr_value <- pr$auc.integral
  
  # Correlation between observed and predicted
  corr_value <- cor(test_data$occrrnS, predicted_probs, method = "pearson")
  
  # -----------------------------
  # PART C: Sweep thresholds to find max TSS
  # -----------------------------
  
  # Helper function to safely compute TSS elements
  compute_tss <- function(obs, preds, threshold) {
    pred_bin <- ifelse(preds >= threshold, 1, 0)
    TP <- sum(pred_bin == 1 & obs == 1)
    TN <- sum(pred_bin == 0 & obs == 0)
    FP <- sum(pred_bin == 1 & obs == 0)
    FN <- sum(pred_bin == 0 & obs == 1)
    
    sens <- if ((TP + FN) > 0) TP / (TP + FN) else NA
    spec <- if ((TN + FP) > 0) TN / (TN + FP) else NA
    tss_val <- sens + spec - 1
    return(list(sensitivity = sens, specificity = spec, TSS = tss_val))
  }
  
  thresholds <- seq(0, 1, by = tss_step)
  tss_df <- data.frame(
    threshold   = thresholds,
    sensitivity = NA,
    specificity = NA,
    TSS         = NA
  )
  
  for (i in seq_along(thresholds)) {
    res_tss <- compute_tss(test_data$occrrnS, predicted_probs, thresholds[i])
    tss_df$sensitivity[i] <- res_tss$sensitivity
    tss_df$specificity[i] <- res_tss$specificity
    tss_df$TSS[i]         <- res_tss$TSS
  }
  
  # Identify the threshold that yields the maximum TSS
  max_idx <- which.max(tss_df$TSS)
  best_threshold <- tss_df$threshold[max_idx]
  best_tss       <- tss_df$TSS[max_idx]
  best_sens      <- tss_df$sensitivity[max_idx]
  best_spec      <- tss_df$specificity[max_idx]
  
  # -----------------------------
  # PART D: Return all metrics
  # -----------------------------
  return(list(
    # The fitted model + raw predictions
    model             = model,
    predicted_probs   = predicted_probs,
    roc_obj           = roc_curve,
    auc               = as.numeric(auc_value),
    aupr              = as.numeric(aupr_value),
    corr              = corr_value,
    confusion_matrix_0.5  = conf_mat,
    metrics_0.5 = data.frame(
      Accuracy     = accuracy,
      Sensitivity  = sensitivity,  # Recall
      Specificity  = specificity,
      Precision    = precision,
      F1           = f1
    ),
    # TSS sweep results
    tss_table      = tss_df,
    best_threshold = best_threshold,
    max_tss        = best_tss,
    best_sensitivity = best_sens,
    best_specificity = best_spec
  ))
}

Run models with our three pairs of data and extract the evaluation metrics of these models.

  • Split_90_absence_unwt: split_90_train & split_90_test

  • Split_70_absence_unwt: split_70_train & split_70_test

  • Split_50_absence_unwt: split_50_train & split_50_test

‘unwt’ means unweighted.

# Apply the fit_model_and_get_perf_no_wt function to train and test lists
model_including_true_absence_no_wt <- mapply(fit_model_and_get_perf_no_wt, 
                   train_data_env = train_list, 
                   test_data_env = test_list,
                   SIMPLIFY = FALSE)

# Build a data frame by extracting each metric from the results
results_including_true_absence_table_no_wt <- data.frame(
  AUC              = sapply(model_including_true_absence_no_wt, function(x) x$auc),
  AUPR             = sapply(model_including_true_absence_no_wt, function(x) x$aupr),
  CORR             = sapply(model_including_true_absence_no_wt, function(x) x$corr),
  Accuracy         = sapply(model_including_true_absence_no_wt, function(x) x$metrics_0.5$Accuracy),
  Sensitivity      = sapply(model_including_true_absence_no_wt, function(x) x$metrics_0.5$Sensitivity),  # Recall
  Specificity      = sapply(model_including_true_absence_no_wt, function(x) x$metrics_0.5$Specificity),
  Precision        = sapply(model_including_true_absence_no_wt, function(x) x$metrics_0.5$Precision),
  F1               = sapply(model_including_true_absence_no_wt, function(x) x$metrics_0.5$F1),
  Best_Threshold   = sapply(model_including_true_absence_no_wt, function(x) x$best_threshold),
  Max_TSS          = sapply(model_including_true_absence_no_wt, function(x) x$max_tss),
  Best_Sensitivity = sapply(model_including_true_absence_no_wt, function(x) x$best_sensitivity),
  Best_Specificity = sapply(model_including_true_absence_no_wt, function(x) x$best_specificity)
)

We can print the evaluation metrics of all three models in one table.

# Round numeric values to 3 decimal places
results_including_true_absence_table_no_wt <- results_including_true_absence_table_no_wt %>%
  mutate(across(where(is.numeric), ~ round(.x, 3)))

# Create the table with smaller font
results_including_true_absence_table_no_wt %>%
  kable("html", caption = "Model Evaluation Metrics") %>%
  kable_styling(font_size = 12, full_width = FALSE)
Model Evaluation Metrics
AUC AUPR CORR Accuracy Sensitivity Specificity Precision F1 Best_Threshold Max_TSS Best_Sensitivity Best_Specificity
split_90_train 0.661 0.645 0.143 0.5 1 0 0.5 0.667 0.97 0.172 0.852 0.320
split_70_train 0.695 0.688 0.325 0.5 1 0 0.5 0.667 0.94 0.284 0.716 0.568
split_50_train 0.664 0.643 0.317 0.5 1 0 0.5 0.667 0.89 0.309 0.882 0.426

3.2.1 Which model is better?

split_70_train shows better overall performance based on AUC, AUPR, CORR, and Best_Specificity.

split_50_train leads in Max_TSS and Best_Sensitivity, indicating it may perform slightly better in balancing true positive and true negative rates.

split_90_train consistently underperforms in most metrics.

🚨Please note that the differences in performance are not substantial, and the choice of the best model may depend on the specific evaluation metric or the trade-offs between them.🚨

3.2.2 Is more always better?

Not necessarily — more true-absence data can help, but only up to a point. The results show that increasing the training data (from 50% to 90%) does not consistently improve the model’s performance. Here’s why:

Performance Improvement with More Absences:

  • As we increased the proportion of true-absence data from 10% (split_90) to 50% (split_50), there was a clear improvement in several metrics:

  • AUC rose from 0.661 (split_90) to 0.695 (split_70), showing better discriminatory power with more absences.

  • AUPR improved similarly, reflecting better precision-recall balance.

  • Max_TSS increased from 0.172 (split_90) to 0.309 (split_50), indicating a better trade-off between sensitivity and specificity.

Diminishing Returns Beyond a Point:

While moving from 10% to 30% absences (split_90 to split_70) resulted in noticeable improvements, the jump from 30% to 50% (split_70 to split_50) offered smaller gains in AUC and AUPR, suggesting diminishing returns.

3.2.3 How much true-absence data is enough?

30% (split_70) seems to strike a good balance:

  • It achieved the highest AUC (0.695) and AUPR (0.688).

  • Best_Specificity (0.568) was highest in split_70, showing better negative prediction performance.

  • Max_TSS (0.284) is respectable and close to the best value (0.309 in split_50).

50% (split_50) provides the highest TSS (0.309) and Best_Sensitivity (0.882) but doesn’t outperform split_70 on AUC and AUPR. This suggests that too much absence data may dilute the signal and introduce noise.

🚨 Please note that these are the primary results and comparisons of models without addressing the imbalanced data issue. Next, we will investigate whether applying weights improves the models and leads to different performance outcomes. 🚨

3.3 Weighted models

As explained in Section 1.2 Weighting methods, we will use a weighting approach to assign more importance to the minority class. To implement this, we adjusted the model code by adding a ‘wt’ parameter and incorporated it into the GLM model.

fit_model_and_get_perf_wt <- function(train_data_env, test_data_env, tss_step = 0.01) {
  
  # Load required libraries
  library(pROC)    # For AUROC
  library(PRROC)   # For AUPR
  
  # 1) Copy data
  train_data <- train_data_env
  test_data  <- test_data_env
  
  # Convert occrrnS to 0/1 numeric
  train_data$occrrnS <- ifelse(train_data$occrrnS == "PRESENT", 1, 0)
  test_data$occrrnS  <- ifelse(test_data$occrrnS == "PRESENT", 1, 0)
  
  # 2) Calculate weights: presence gets 1; background gets (prNum / bgNum)
  prNum <- sum(train_data$occrrnS == 1)
  bgNum <- sum(train_data$occrrnS == 0)
  wt <- ifelse(train_data$occrrnS == 1, 1, prNum / bgNum)
  
  # 3) Fit the weighted GLM
  my_formula <- occrrnS ~ 
    `AusClim_bioclim_03_9s_1976-2005` + 
    `AusClim_bioclim_06_9s_1976-2005` + 
    `AusClim_bioclim_09_9s_1976-2005` + 
    `AusClim_bioclim_15_9s_1976-2005` + 
    `AusClim_bioclim_24_9s_1976-2005` + 
    `AusClim_bioclim_27_9s_1976-2005` + 
    `AusClim_bioclim_29_9s_1976-2005`
  
  model <- glm(my_formula, data = train_data, weights = wt, family = binomial(link = "logit"))
  
  # Predict probabilities
  predicted_probs <- predict(model, newdata = test_data, type = "response")
  
  # -----------------------------
  # PART A: Standard metrics at threshold = 0.5
  # -----------------------------
  pred_class <- ifelse(predicted_probs >= 0.5, 1, 0)
  
  # Force table to have both '0' and '1' levels
  pred_class_factor <- factor(pred_class, levels = c(0,1))
  actual_factor     <- factor(test_data$occrrnS, levels = c(0,1))
  
  conf_mat <- table(Predicted = pred_class_factor, Actual = actual_factor)
  
  # Safely extract entries
  TP <- conf_mat["1","1"]
  FP <- conf_mat["1","0"]
  FN <- conf_mat["0","1"]
  TN <- conf_mat["0","0"]
  
  # Compute standard metrics
  accuracy    <- (TP + TN) / sum(conf_mat)
  sensitivity <- TP / (TP + FN)  # Recall
  specificity <- TN / (TN + FP)
  precision   <- TP / (TP + FP)
  f1          <- 2 * precision * sensitivity / (precision + sensitivity)
  
  # -----------------------------
  # PART B: Additional Metrics
  # -----------------------------
  
  # AUROC
  roc_curve <- pROC::roc(response = test_data$occrrnS, predictor = predicted_probs)
  auc_value <- pROC::auc(roc_curve)
  
  # AUPR (Area Under Precision-Recall Curve)
  pr <- pr.curve(scores.class0 = predicted_probs[test_data$occrrnS == 1],
                 scores.class1 = predicted_probs[test_data$occrrnS == 0],
                 curve = TRUE)
  aupr_value <- pr$auc.integral
  
  # Correlation between observed and predicted
  corr_value <- cor(test_data$occrrnS, predicted_probs, method = "pearson")
  
  # -----------------------------
  # PART C: Sweep thresholds to find max TSS
  # -----------------------------
  compute_tss <- function(obs, preds, threshold) {
    pred_bin <- ifelse(preds >= threshold, 1, 0)
    TP <- sum(pred_bin == 1 & obs == 1)
    TN <- sum(pred_bin == 0 & obs == 0)
    FP <- sum(pred_bin == 1 & obs == 0)
    FN <- sum(pred_bin == 0 & obs == 1)
    
    sens <- if ((TP + FN) > 0) TP / (TP + FN) else NA
    spec <- if ((TN + FP) > 0) TN / (TN + FP) else NA
    tss_val <- sens + spec - 1
    return(list(sensitivity = sens, specificity = spec, TSS = tss_val))
  }
  
  thresholds <- seq(0, 1, by = tss_step)
  tss_df <- data.frame(
    threshold   = thresholds,
    sensitivity = NA,
    specificity = NA,
    TSS         = NA
  )
  
  for (i in seq_along(thresholds)) {
    out_tss <- compute_tss(test_data$occrrnS, predicted_probs, thresholds[i])
    tss_df$sensitivity[i] <- out_tss$sensitivity
    tss_df$specificity[i] <- out_tss$specificity
    tss_df$TSS[i]         <- out_tss$TSS
  }
  
  # Identify threshold that yields the maximum TSS
  max_idx <- which.max(tss_df$TSS)
  best_threshold <- tss_df$threshold[max_idx]
  best_tss       <- tss_df$TSS[max_idx]
  best_sens      <- tss_df$sensitivity[max_idx]
  best_spec      <- tss_df$specificity[max_idx]
  
  # -----------------------------
  # PART D: Return all metrics
  # -----------------------------
  return(list(
    # Model and predictions
    model              = model,
    predicted_probs    = predicted_probs,
    roc_obj            = roc_curve,
    
    # Evaluation Metrics
    auc                = as.numeric(auc_value),   # AUROC
    aupr               = as.numeric(aupr_value),  # AUPR
    corr               = corr_value,              # Correlation
    
    # Confusion Matrix at threshold 0.5
    confusion_matrix_0.5 = conf_mat,
    
    # Metrics at threshold 0.5
    metrics_0.5 = data.frame(
      Accuracy     = accuracy,
      Sensitivity  = sensitivity,  # Recall
      Specificity  = specificity,
      Precision    = precision,
      F1           = f1
    ),
    
    # TSS sweep results
    tss_table      = tss_df,
    best_threshold = best_threshold,
    max_tss        = best_tss,
    best_sensitivity = best_sens,
    best_specificity = best_spec
  ))
}

Run models with our three pairs of data and extract the evaluation metrics of these models.

  • Split_90_absence_wt: split_90_train & split_90_test

  • Split_70_absence_wt: split_70_train & split_70_test

  • Split_50_absence_wt: split_50_train & split_50_test

‘wt’ means weighted.

# 1) Fit weighted models for each train/test pair
model_including_true_absence_wt <- mapply(
  fit_model_and_get_perf_wt,
  train_data_env = train_list,
  test_data_env  = test_list,
  SIMPLIFY       = FALSE
)

# 2) Build a data frame by extracting each metric from the results
#    Note: 'metrics_0.5' is where threshold=0.5 metrics live.
results_including_true_absence_table_wt <- data.frame(
  AUC              = sapply(model_including_true_absence_wt, function(x) x$auc),                   # AUROC
  AUPR             = sapply(model_including_true_absence_wt, function(x) x$aupr),                  # AUPR
  CORR             = sapply(model_including_true_absence_wt, function(x) x$corr),                  # Correlation
  Accuracy         = sapply(model_including_true_absence_wt, function(x) x$`metrics_0.5`$Accuracy),
  Sensitivity      = sapply(model_including_true_absence_wt, function(x) x$`metrics_0.5`$Sensitivity),  # Recall
  Specificity      = sapply(model_including_true_absence_wt, function(x) x$`metrics_0.5`$Specificity),
  Precision        = sapply(model_including_true_absence_wt, function(x) x$`metrics_0.5`$Precision),
  F1               = sapply(model_including_true_absence_wt, function(x) x$`metrics_0.5`$F1),
  Best_Threshold   = sapply(model_including_true_absence_wt, function(x) x$best_threshold),
  Max_TSS          = sapply(model_including_true_absence_wt, function(x) x$max_tss),
  Best_Sensitivity = sapply(model_including_true_absence_wt, function(x) x$best_sensitivity),
  Best_Specificity = sapply(model_including_true_absence_wt, function(x) x$best_specificity)
)

We can print the evaluation metrics of all three models in one table.

# Round numeric values to 3 decimal places
results_including_true_absence_table_wt <- results_including_true_absence_table_wt %>%
  mutate(across(where(is.numeric), ~ round(.x, 3)))

# Create the table with smaller font
results_including_true_absence_table_wt %>%
  kable("html", caption = "Model Evaluation Metrics") %>%
  kable_styling(font_size = 12, full_width = FALSE)
Model Evaluation Metrics
AUC AUPR CORR Accuracy Sensitivity Specificity Precision F1 Best_Threshold Max_TSS Best_Sensitivity Best_Specificity
split_90_train 0.679 0.678 0.281 0.607 0.779 0.434 0.579 0.664 0.65 0.295 0.557 0.738
split_70_train 0.697 0.690 0.336 0.647 0.674 0.621 0.640 0.656 0.49 0.295 0.705 0.589
split_50_train 0.670 0.647 0.297 0.588 0.588 0.588 0.588 0.588 0.45 0.324 0.838 0.485

3.4 Comparing un-weighted and weighted methods.

We combine the performance tables of un-weighted and weighted models to see the differences between these two methods.

#combine two evaluation tables
combined_df <- bind_rows(
  results_including_true_absence_table_no_wt %>%
    mutate(Source = "No_WT"),
  results_including_true_absence_table_wt %>%
    mutate(Source = "WT")
) %>%
  mutate(across(where(is.numeric), ~ round(.x, 3)))

# Change order of columsn so that Source is the first column
combined_df <- combined_df %>%
  dplyr::select(Source, everything())

# Create the table using row names
kable(combined_df, "html", caption = "Model Evaluation Metrics", rownames = TRUE) %>%
  kable_styling(font_size = 12, full_width = FALSE)
Model Evaluation Metrics
Source AUC AUPR CORR Accuracy Sensitivity Specificity Precision F1 Best_Threshold Max_TSS Best_Sensitivity Best_Specificity
split_90_train...1 No_WT 0.661 0.645 0.143 0.500 1.000 0.000 0.500 0.667 0.97 0.172 0.852 0.320
split_70_train...2 No_WT 0.695 0.688 0.325 0.500 1.000 0.000 0.500 0.667 0.94 0.284 0.716 0.568
split_50_train...3 No_WT 0.664 0.643 0.317 0.500 1.000 0.000 0.500 0.667 0.89 0.309 0.882 0.426
split_90_train...4 WT 0.679 0.678 0.281 0.607 0.779 0.434 0.579 0.664 0.65 0.295 0.557 0.738
split_70_train...5 WT 0.697 0.690 0.336 0.647 0.674 0.621 0.640 0.656 0.49 0.295 0.705 0.589
split_50_train...6 WT 0.670 0.647 0.297 0.588 0.588 0.588 0.588 0.588 0.45 0.324 0.838 0.485

3.4.2 Summary

Metric Unweighted Weighted
Sensitivity Very high (1.0) but at the expense of specificity. Balanced (~0.58 - 0.77).
Specificity Extremely poor (0.0). Improved (~0.43 - 0.62).
AUC / AUPR Moderate (0.66 - 0.69). Similar or slightly better (0.67 - 0.70).
F1 Score Inflated due to perfect recall but low precision. More balanced (~0.59 - 0.66).
TSS Low (~0.17 - 0.31), poor model skill. Higher (~0.29 - 0.32), indicating improved skill.

Weighting improved overall model performance, especially in addressing the imbalance between presences and absences.

The split_70_train (WT) appears to be the most balanced and effective model.

While sensitivity decreased, the gains in specificity, and TSS suggest more reliable and generalisable 

We should always consider weighting methods when the species binary dataset has an imbalance issue.

4 Summary

Addressing imbalanced species data is crucial for producing reliable and accurate Species Distribution Models. In part 1 we showcased, via the Gang-gang Cockatoo case study, how to used weighted models to improve the performance of SDMs. While for some metrics the differences between weighted and unweighted models were not substantial, the weighted models better addressed the class imbalance issue, leading to more balanced and interpretable results. Ultimately, integrating these techniques into ecological modeling workflows supports better conservation planning and decision-making, ensuring more robust and interpretable SDMs within platforms like EcoCommons.

References

Barbet-Massin, M., Jiguet, F., Albert, C., & Thuiller, W. (2012). Selecting pseudo-absences for species distribution models: How, where and how many? Methods ecol evol 3: 327–338.
Benkendorf, D. J., Schwartz, S. D., Cutler, D. R., & Hawkins, C. P. (2023). Correcting for the effects of class imbalance improves the performance of machine-learning based species distribution models. Ecological Modelling, 483, 110414.
Chawla, N. V., Bowyer, K. W., Hall, L. O., & Kegelmeyer, W. P. (2002). SMOTE: Synthetic minority over-sampling technique. Journal of Artificial Intelligence Research, 16, 321–357.
Chen, C., Liaw, A., Breiman, L., et al. (2004). Using random forest to learn imbalanced data. University of California, Berkeley, 110(1-12), 24.
Elith*, J., H. Graham*, C., P. Anderson, R., Dudı́k, M., Ferrier, S., Guisan, A., J. Hijmans, R., Huettmann, F., R. Leathwick, J., Lehmann, A., et al. (2006). Novel methods improve prediction of species’ distributions from occurrence data. Ecography, 29(2), 129–151.
Gaul, W., Sadykova, D., White, H. J., León-Sánchez, L., Caplat, P., Emmerson, M. C., & Yearsley, J. M. (2022). Modelling the distribution of rare invertebrates by correcting class imbalance and spatial bias. Diversity and Distributions, 28(10), 2171–2186.
Johnson, R. A., Chawla, N. V., & Hellmann, J. J. (2012). Species distribution modeling and prediction: A class imbalance problem. 2012 Conference on Intelligent Data Understanding, 9–16.
Menardi, G., & Torelli, N. (2014). Training and assessing classification rules with imbalanced data. Data Mining and Knowledge Discovery, 28, 92–122.
Václavı́k, T., & Meentemeyer, R. K. (2009). Invasive species distribution modeling (iSDM): Are absence data and dispersal constraints needed to predict actual distributions? Ecological Modelling, 220(23), 3248–3258.
Valavi, R., Guillera-Arroita, G., Lahoz-Monfort, J. J., & Elith, J. (2022). Predictive performance of presence-only species distribution models: A benchmark study with reproducible code. Ecological Monographs, 92(1), e01486.
Zhang, Z., Mammola, S., & Zhang, H. (2020). Does weighting presence records improve the performance of species distribution models? A test using fish larval stages in the yangtze estuary. Science of The Total Environment, 741, 140393.
footer

Section Break

EcoCommons received investment (https://doi.org/10.3565/chbq-mr75) from the Australian Research Data Commons (ARDC). The ARDC is enabled by the National Collaborative Research Infrastructure Strategy (NCRIS).

Our Partner

Partners Logos

How to Cite EcoCommons

If you use EcoCommons in your research, please cite the platform as follows:

EcoCommons Australia 2024. EcoCommons Australia – a collaborative commons for ecological and environmental modelling, Queensland Cyber Infrastructure Foundation, Brisbane, Queensland. Available at: https://data–explorer.app.ecocommons.org.au/ (Accessed: MM DD, YYYY). https://doi.org/10.3565/chbq-mr75

You can download the citation file for EcoCommons Australia here: Download the BibTeX file

© 2024 EcoCommons. All rights reserved.